Exploiting bad randomness for the rarest NFTs
github.com/tfire/salted-pretzel
Abstract
This writing details an approach to gaming onchain randomness, specifically in the case of generative NFTs. Pseudo-random factors are combined and passed through keccak256 to produce a hash used to map traits (therefore rarity) to the minted NFT. By controlling one or more of the factors included as input to the hash function, we can optimize for a hash that produces traits of significantly high rarity, and thus higher economic “value.”
Situational Mechanics
There is 1 specific mechanic to our particular environment which makes it more complex than just a minting. The additional complexities built into the attack to account for this mechanic could be removed to utilize the elements of the exploit in another environment. The particular mechanic is this:
- In order for a user to mint, they must have ownership of a
Permission TokenNFT.
Additional specifics:
- The code mapping a hash to its traits is stored onchain as retrievable JavaScript. This seems to be a common pattern in a variety of projects.
Hashing
There are 4 items packed and passed to keccak256:
- minting address
- block number
- block difficulty
- mint number
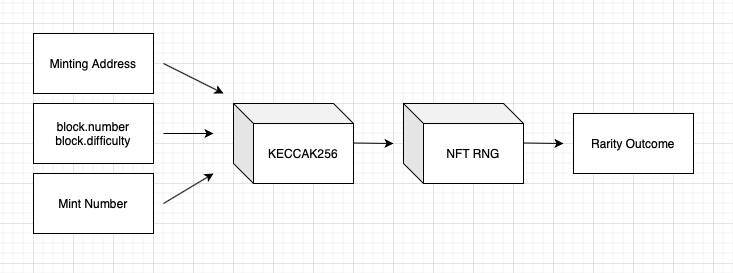
Minting address is known. Block number is wholly predictable, of course. Block difficulty is pseudo-random, but calcuable (and in TypeScript.) Mint number is retrievable with a web request to Etherscan in <200ms, or faster with a geth full node.
Given Unlimited Funds and Unlimited Time
One potential way this system could be manipulated is if the NFT RNG function was converted to Solidity and deployed onchain alongside some exploit logic.
Send a transaction at each new block to the attacking contract. The attacking contract should redeem the mint, retrieve the hash that the minting contract created, and run the onchain RNG against it. If the outcome is unfavorable, revert the transaction.
Alternatively, generate the hash without initiating a mint, as the attacking contract has access to the instantaneous block.difficulty value as well. Run the created hash against the RNG. If the outcome is favorable, then initiate a mint.
The problem with either of these approaches is that they are completely cost-ineffective. Given 1/1000 odds, it would take on average 999 failed transactions and all the associated gas costs.
Given No Funds and No Time…
We now jump from something completely infeasible to improving this attack to the point of instantaneous perfect odds at any block.
As a reminder, the hash parameters are: block.number, block.difficulty, mint number, minting address.
block.number, block.difficulty
The next block number is always known when a block header is received, as blockheader.number + 1.
The ethhash difficulty computation is essentially a function of the timestamp at which the block is mined. Offchain, one can calculate the difficulty for the next i.e. 30 timestamps (seconds). Conveniently, the same difficulty value will typically span 5-6 consecutive timestamps, reducing total offchain computation necessary.
Mint number
This is a public view on the NFT contract. We retrieved this with a web request to web3api.com. The same could be done with a local geth node, although in our case a node running in --light mode failed to access this data, even from its peers.
Minting address
This is the initiator and recipient of the mint. It must be fixed and static as the owner of the Permission Token.
Unless..?
Leveraging CREATE2
CREATE2 is an EVM opcode that allows you to deploy a contract to a deterministic address by providing a salt. This is the heart of the exploit. Rather than waiting 1000+ blocks and “sniping” a suitable block.number/block.difficulty combination, we instead isolate the minting address as the manipulable parameter to the hash function for instantaneous perfect odds at any block.
As a reminder, the RNG JavaScript is available onchain. We take it from the chain and run it locally.
The general offchain algorithm is as follows:
compute difficulties for next block
for each possible difficulty:
for (salt = 0; salt++)
addr = CREATE2(salt, ...)
hash = keccak(block.number, difficulty, mint.number, addr)
if RNG(hash) is good
save salt
break
Master and Slave Contracts
In order to execute a CREATE2 opcode, we need to be onchain. This implies 2 layers of contract deployment.
Preparation:
- Manually deploy a Master contract that implements ERC721-receiver. Transacting with the Master contract deploys a Slave contract that also implements ERC721-receiver. This Slave contract is deployed at a deterministic address as a function of a salt value.
- Send the
Permission Tokento the Master contract.
Execution:
- Transact with the Master contract, providing in the calldata an array of salts indexed by
block.timestamp - parentTimestamp. The salt at this index corresponds to the salt that will create an address which, when combined with the difficulty at block.timestamp, the block number, and the mint number, produces a hash that results in a favorable RNG outcome. - Master deploys a Slave using CREATE2 and the salt at the provided index.
- Master transfers the
Permission Tokento the deployed Slave. - Slave transacts with NFT contract and receives a favorable mint.
- Slave transfers
Permission TokenandFavorable Mintback to Master or another EOA.
All of the above execution has occurred in a single transaction, peppered with require() calls to ensure that the block difficulty matches what was computed offchain, that the Slave address is as expected, and that the final location of both NFTs is correct. Any failure for these requirements to be met will revert the transaction.
Conclusion and Solution
We’ve shown here how bad onchain pseudo-randomness can be exploited to procure NFT mints of high rarity or selectable traits with odds of 100% and in 1 transaction.
Solutions to patch this problem:
- Trivial: Bottleneck the offchain RNG by hashing the hash with pbkdf2, used to remedy such brute force attacks.
- Non-trivial: Implement a commit/reveal scheme. This approach has not been fully investigated in particular context.
Source code: github.com/tfire/salted-pretzel